Scattering of Electrons in Matter
| "If, in some cataclysm, all of scientific knowledge were to be destroyed, and only one sentence passed on to the next generations of creatures, what statement would contain the most information in the fewest words? I believe it is the atomic hypothesis...that all things are made of atoms-little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. In that one sentence, you will see, there is an enormous amount of information about the world, if just a little imagination and thinking are applied." |
| -- Richard Feynman |
INTRODUCTION
By the early part of the 20th century, the existence of atoms was not seriously in doubt, but little was known about their structure. Experiments had shown that electrons exist and come from atoms. These particles have very small mass (compared to that of the atom as a whole) and negative electric charge. Clearly there must be something else inside the atom, since most of the mass cannot be accounted for by electrons alone. Furthermore, since atoms are electrically neutral, some part of the atom must have a compensating positive charge. The questions were: what is this positively-charged "stuff"; and how are it and the electrons put together to make an atom?
One popular theory, called the "plum pudding" model, had the negatively charged electrons embedded like plums in a "pudding" of positive charge. (Think of negatively charged chocolate chips in positively charged cookie dough, if you like.) The atom was static, with the electrons at rest in the "pudding."
Ernest Rutherford and his collaborators Marsden and Geiger (of Geiger counter fame) settled this question in a series of classic experiments carried out between 1908 and 1913. They bombarded thin foils of gold and other materials with heavy "alpha particles," and observed how these were scattered. Interestingly, some of the particles bounced straight back from the foil. Rutherford concluded that the only way this was possible was if the positive charge and most of the mass was concentrated in a tiny region at the center of the atom, which he called the "nucleus," and not spread out as in the plum pudding model. Only such a concentrated region of mass and charge could provide the strong repulsion needed to turn the bombarding particles around and send them back.
This immediately raised a new question: What keeps the negatively charged electrons from being attracted to the positively charged nucleus and falling into it? Rutherford proposed a model in which the atom behaves like a miniature solar system: the electrons move around the nucleus fast enough that their momentum keeps them in orbit against the attractive force of the opposite charges. Unlike the plum pudding model, Rutherford's atom is dynamic;the electrons are constantly in motion. Also, unlike its competitors it is correct. Literally thousands of experiments have since confirmed this basic picture of the atom. In fact Rutherford's discovery went well beyond providing a snapshot of the atom; his results had extremely important consequences for the further development of physics. His experiments are thus among the most important in the history of science.
THE PROJECT
 In this project we will consider a variation on Rutherford's theme and develop a simulation of a beam of electrons bombarding a thin foil of some material. This basic process underlies the operation of a number of modern devices, including Scanning and Transmission Electron Microscopes (SEM and TEM). The basic idea behind these is to use the pattern of scattered electrons to reconstruct a picture of the object under study.
In this project we will consider a variation on Rutherford's theme and develop a simulation of a beam of electrons bombarding a thin foil of some material. This basic process underlies the operation of a number of modern devices, including Scanning and Transmission Electron Microscopes (SEM and TEM). The basic idea behind these is to use the pattern of scattered electrons to reconstruct a picture of the object under study.
As they wend their way through the foil, the electrons interact with the foil atoms in various ways, losing energy and bouncing off the nuclei in different directions. Some fraction of them eventually make it through the foil, some fraction are reflected, and a few wind up losing so much energy that they are captured. The goal of our simulation will be to calculate these fractions. We can then compare the predictions of our model to actual laboratory data, to see how well it works.
The heart of the simulation is the basic physics that governs how the electrons interact with the foil atoms. These are equations of "quantum mechanics," which determine how much energy is lost and how much the direction changes in a single collision. Ultimately it is these laws that determine the fractions of transmitted, reflected and captured electrons.
To calculate these fractions we will use the Monte Carlo technique. This is a popular approach to solving complex problems, and has as its basic feature the averaging of a large number of random events. To take a simple example, consider the problem of determining the value of pi. A typical Monte Carlo approach might begin by drawing a square with a circle inscribed in it:

The circle has radius R, and the square has sides of length 2R.
Now imagine throwing darts randomly in the square. After many darts have been thrown, the ratio of the number of darts that land in the circle to the total number of darts will be about the same (if the darts really are thrown randomly!) as the ratio of the area of the circle to the area of the square. But this ratio is just

So by counting the fraction of darts that land in the circle, and multiplying by four, we get an approximate value for pi. The approximation gets better and better the more darts we use.
In our problem we will consider a large number of electrons and follow each one as it works its way through the foil. As it travels, each electron bounces randomly off the atoms in the foil according to known quantum-mechanical interactions. Ultimately it will either escape, be reflected, or be captured. After simulating a large number of electrons, the resulting fractions of each type of particle should be a good approximation to the actual transmission, reflection and capture rates predicted by the model.
VISUALIZATION
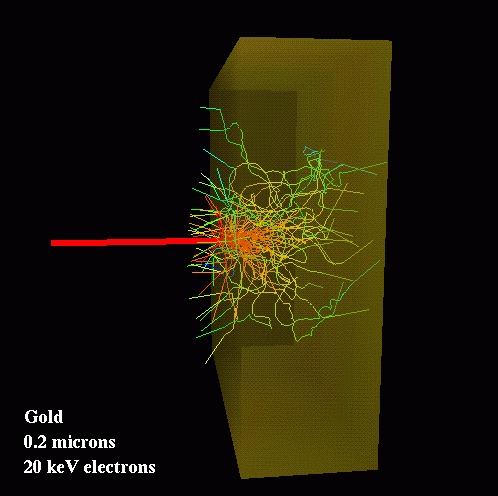
We will be using AVS/Express to visualize our results in various ways. One interesting possibility is to create images of particle tracks in the foil. This example shows the tracks of 70 electrons as they impact a thin foil of gold. The incoming beam is represented by the heavy red line. The colors of the tracks indicates the energies of the particles, with red being higher and blue lower values. On average, each electron undergoes several hundred collisions before escaping the foil.
ANIMATIONS
SI2004
SI2000
SI1999
Dave Robertson is the OSC coordinator for the Electron Scattering project.
For assistance, write si-contact@osc.edu or call 614-292-0890.